二项式系数¶

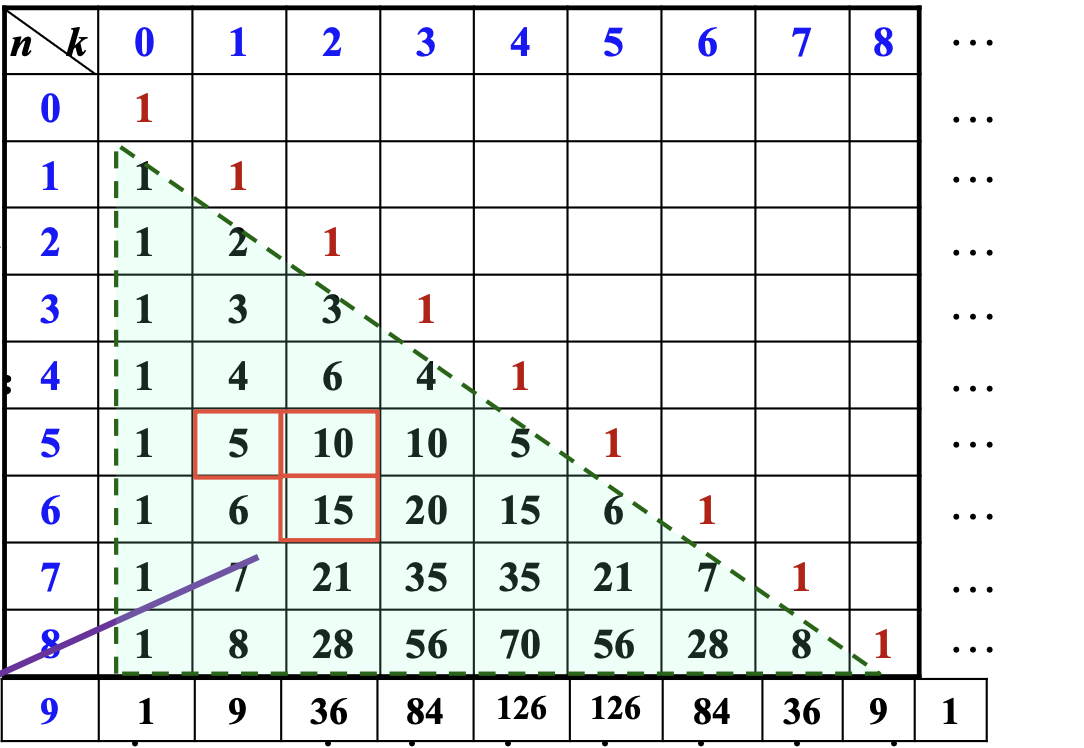
帕斯卡三角形¶

帕斯卡公式: $$ \binom{n}{k} = \binom{n-1}{k} + \binom{n-1}{k-1} $$ 帕斯卡三角形:

$k=3$ 是四面体数，堆起来的金字塔
在只允许向下和向右下走时，$\binom{n}{k}$ 可以看作从 $\binom{0}{0}$ 到 $\binom{n}{k}$ 的路径数

组合推理¶

证明等式的方法:

利用已知公式
求导法&积分法
组合推理法

二项式定理¶

定理

\[ (x+y)^n = x^n + \binom{n}{1}x^{n-1}y + \binom{n}{2} x^{n-2}y^2 + \cdots + \binom{n}{n-1}xy^{n-1} + y^n \]

一些等式:

\[ k \binom{n}{k} = n \binom{n-1}{k-1} \]

从 $n$ 人里选 $k$ 个人组成球队，并且要选一个队长

\[ \sum\limits_{k=0}^{n} \binom{n}{k}^2 = \binom{2n}{n} \]

将 $2n$ 个元素的集合均分为两个集合，共同取出 $n$ 个元素

扩展定义¶

$\binom{n}{k}$ 允许 $n$ 为任意实数，$k$ 为任意整数，则

\[ \binom{n}{k} = \left\{\begin{matrix} & \frac{n(n-1)\cdots(n-k+1)}{k!} & k\geqslant1 \\ & 1 & k = 0\\ & 0 & k \leqslant -1\\ \end{matrix}\right. \]

帕斯卡公式和球队公式 (随便起的名～) 依然成立

反链和最大链*¶

设 $S$ 是 $n$ 元素集合，$S$ 的一个反链是集合 $S$ 的子集的一个集合 $\mathbf{A}$，其中 $\mathbf{A}$ 中的子集不互相包含

容易发现，集合 $S$ 的 $k$ 子集可以构成反链。这种方法构造的反链至多含有 $\binom{n}{\left \lfloor n / 2\right \rfloor}$ 个集合，例如 $S = \{a,b,c,d\}$ 的2子集给出大小为6的反链 $\mathbf{C}_2 = \{\{a, b\}, \{a, c\}, \{a,d\}, \{b, c\}, \{b,d\}, \{c,d\}\}$

链: $S$ 的子集的集合 $\mathbf{C}$ 是一条链，只要对 $\mathbf{C}$ 中的每一对子集，总有一个包含在另一个之中

最大链: 链，包含 $S$ 各种可能大小的子集各一个，可以利用以下方法得到，

定理 设 $S$ 是 $n$ 元素集合，那么 $S$ 上的一个反链至多包含 $\binom{n}{\left \lfloor n / 2\right \rfloor}$ 个集合

证明 设 $\mathbf{A}$ 是一个反链，我们用两种不同的方法计数有序对 $(A, C)$ 的数目 $\beta$，其中 $A$ 在 $\mathbf{A}$ 中，$C$ 是包含 $A$ 的最大链。

因为每个最大链至多包含反链中的一个子集，所以 $\beta$ 至多等于最大链的个数，$\beta \leqslant n!$ 。对于反链中的子集 $A$，如果 $|A| = k$，那么至多存在 $k!(n-k)!$ 个包含 $A$ 的最大链 $C$，设 $a_k$ 是反链中大小为 $k$ 的子集个数，使得 $|\mathbf{A}| = \sum\limits_{k=0}^{n}a_k$ ，于是 $\beta = \sum\limits_{k=0}^{n}a_kk!(n-k)!$，又因为 $\beta \leqslant n!$ ，所以得到

\[ \sum\limits_{k=0}^{n}a_kk!(n-k)! \leqslant n!\\ \sum\limits_{k=0}^{n}a_k \frac{k!(n-k)!}{n!} \leqslant 1\\ \sum\limits_{k=0}^{n}\frac{a_k}{\binom{n}{k}} \leqslant 1 \]

当 $k = \left \lfloor n/2\right \rfloor$ 时，$\binom{n}{k}$ 最大，于是有 $|\mathbf{A}| \leqslant \sum\limits_{k=0}^{n}a_k \leqslant \binom{n}{\left \lfloor n/2\right \rfloor}$

可以证明，如果 $n$ 是偶数，大小为 $\binom{n}{\left \lfloor n/2\right \rfloor}$ 的唯一反链是 $S$ 的所有 $\frac{n}{2}$ 子集构成的，如果 $n$ 是奇数，有 $\frac{n-1}{2}$ 和 $\frac{n+1}{2}$ 子集构成同样大小的反链。

TODO

Take time to understand

多项式定理¶

多项式系数的定义:

\[ \binom{n}{n_1n_2\cdots n_t} = \frac{n!}{n_1!n_2!\cdots n_t!} \]

$n_1, n_2, \cdots, n_t$ 是非负整数且 $n_1 + n_2 + \cdots + n_t = n$

多项式系数的帕斯卡公式:

\[ \binom{n}{n_1n_2\cdots n_t} = \binom{n-1}{n_1-1 \space n_2\cdots n_t} + \binom{n-1}{n_1 \space n_2-1 \cdots n_t} + \cdots + \binom{n-1}{n_1n_2\cdots n_t-1} \]

证明

多项式的展开: $(x_1 + x_2 + x_3)^3 = x_1^3 + x_2^3 + x_3^3 + 3x_1x_2^2 + 3x_1^2x_2+ 3x_1x_3^2 + 3x_1^2x_3 + 3x_2x_3^2 + 3x_2^2x_3 + 6x_1x_2x_3$

定理 $n$ 是正整数，有

\[ (x_1 + x_2 + \cdots + x_t)^n = \sum\binom{n}{n_1n_2\cdots n_t}x_1^{n_1}x_2^{n_2}\cdots x_t^{n_t} \]

其中求和是对 $n_1 + n_2 + \cdots + n_t = n$ 的所有非负整数解进行的

证明 展开并选择，选 $n$ 个因子中 $n_1$ 个 $x_1$，剩下 $n-n_1$ 中选 $n_2$ 个 $x_2$，$\cdots$ ，最终得到 $x_1^{n_1}x_2^{n_2}\cdots x_t^{n_t}$ 项，项的出现次数为

\[ \binom{n}{n_1}\binom{n-n_1}{n_2}\cdots \binom{n-n_1-\cdots -n_{t-1}}{n_t} \]

恰等于多项式系数，QED

牛顿二项式定理¶

定理 设 $\alpha$ 是实数，对于所有满足 $0\leqslant|x|<|y|$ 的 $x$ 和 $y$ ，有 $$ (x+y)^{{\alpha}=\sum\limits_{k=0}}x}\binom{\alpha}{k^ky $$ 其中， $$ \binom{\alpha}{k}=\frac{\alpha(\alpha-1)\cdots(\alpha-k+1)}{k!} $$ 实际上就是把整数指数扩展到了实数